General theory for packing icosahedral shells into multi-component aggregates
Nicolò Canestrari, Diana Nelli and Riccardo Ferrando
https://doi.org/10.1038/s41467-025-56952-1
The sphere packing problem fascinates matematicians and physicists since long time. The starting point was the "cannonball problem" (how to efficiently pile cannonballs in a ship?) posed by the explorer and corsair Sir Walter Raleigh during one of his ocean crossings, which soon led to the study of closed-packed 3D lattices, and then to the formulation of the well-known Kepler conjecture on the maximum packing density of equal spheres (still not incontrovertibly proven). Today, sphere packing problems apply to more complex situations, such as the presence of spheres of unequal size and packing in confined spaces or in discrete aggregates with high symmetry, such as the icosahedron and decahedron.
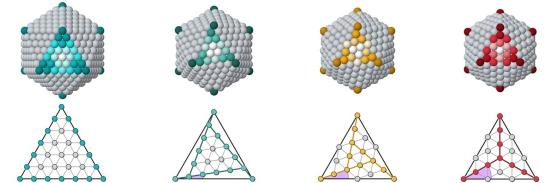
Nicolò Canestrari, Diana Nelli and Riccardo Ferrando, from the Nanobiocomp group at DIFI, studied the packing of atoms into compact clusters, and proposed a general theory for building multi-component icosahedral structures by assembling concentric chiral and achiral shells of particles. The authors established simple and general rules for designing a wide variety of magic icosahedral structures, and for evaluating the optimal size-mismatch between particles in the different shells. The authors also performed molecular dynamics simulations to investigate the formation of different multi-metallic clusters, showing that the icosahedral shell sequences predicted by their design strategy spontaneosly self-assemble during growth.
This work paves the way for the design of new multi-component structures made of particles of different types, such as metallic nanoparticles, aggregates of colloidal particles and of complex molecules of biological interest.


